01_线性结构

577

线性结构是一种基本的数据结构，主要用于对客观世界中具有单一前驱和后继的数据关系 进行描述。线性结构的特点是数据元素之间呈现一种线性关系，即元素“一个接一个排列”。

一、线性表

线性表是最简单、最基本也是最常用的一种线性结构。常采用顺序存储和链式存储，主要 的基本操作是插入、删除和查找等。

1. 线性表的定义

一个线性表是n(n≥0) 个元素的有限序列，通常表示为 (a₁,a₂,…,an) 。  非空线性表的特点如下。

  1. 存在唯一的一个称作“第一个”的元素。
  2. 存在唯一的一个称作“最后一个”的元素。
  3. 除第一个元素外，序列中的每个元素均只有一个直接前驱。
  4. 除最后一个元素外，序列中的每个元素均只有一个直接后继。

2. 线性表的存储结构

线性表的存储结构分为顺序存储和链式存储。

线性表的顺序存储

线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表 中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻，如 图3-1所示。在这种存储方式下，元素间的逻辑关系无须占用额外的空间 来存储。

线性表的链式存储

线性表的链式存储是用通过指针链接起来的结点来存储数据元素，基本的结点结构如下所示：

数据域 指针域

其中，数据域用于存储数据元素的值，指针域则存储当前元素的直接前驱或直接后继的位置信 息，指针域中的信息称为指针(或链),

存储各数据元素的结点的地址并不要求是连续的，因此存储数据元素的同时必须存储元素之间的逻辑关系。另外，结点空间只有在需要的时候才申请，无须事先分配。

结点之间通过指针域构成一个链表，若结点中只有一个指针域，则称为线性链表(或单链 表),如图3-2所示。
image.png

图3-2 线性表的单链表存储 

设线性表中的元素是整型，则 #单链表结点类型的定义# 为：

typedef struct node{
	int data;              /*结点的数据域，此处假设为整形*/
	struct node *next;     /*结点的指针域*/
}NODE,*LinkList

在链式存储结构中，只需要一个指针(称为头指针，如图3-2中的head)  指向第一个结点， 就可以顺序地访问到表中的任意一个元素。

在 #链式存储结构下进行插入和删除# ，其实质都是对相关指针的修改。在单链表中，若在 p 所指结点后插入新元素结点 (s 所指结点，已经生成),如图3-3 (a) 所示，其基本步骤如下。

s->next=p->next;
p->next=s;

即先将p 所指结点的后继结点指针赋给s 所指结点的指针域，然后将p 所指结点的指针域 修改为指向s 所指结点。
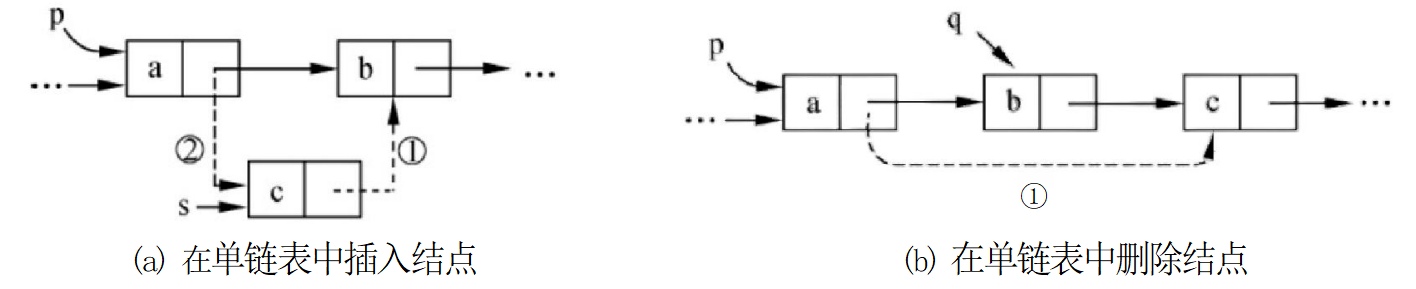
​image.png

图3-3 在单链表中插入、删除结点时的指针变化示意图

同理，在单链表中删除p 所指结点的后继结点时(如图3-3 (b)   所示),步骤如下。

q=p->next;
p->next=p->next->next;
free(q);

即先令临时指针q 指向待删除的结点，然后修改p 所指结点的指针域为指向p 所指结点的 后继的后继结点，从而将元素b 所在的结点从链表中删除，最后释放q 所指结点的空间。

在实际应用中，为了简化对链表状态的判定和处理，特别引入一个不存储数据元素的结点， 称为头结点，将其作为链表的第一个结点并令头指针指向该结点。

[!example]+ #【函数】单链表的查找运算#

LinkList Find_List(LinkList L,int k)     /*L为带头结点单链表的头指针*/
/*在表中查找第k 个元素，若找到，返回该元素结点的指针；否则，返回空指针 NULL*/
{   LinkList p;int i;i = 1; p = L->next;                /*初始时，令p 指向第一个元素结点，i  为计数器*/
	while(p&&i<k){               /*顺指针链向后查找，直到p 指向第k 个元素结点或p 为空指针*/
		p=p->next;i++; }
	if(p&&i==k)return p;     /* 存在第k 个元素且指针p 指向该元素结点*/
	return NULL;                        /*第k 个元素不存在，返回空指针*/
}/*Find_List*/

[!example] #【函数】单链表的插入运算#

int Insert_List (LinkList L,int k,int newElem)    /*L为带头结点单链表的头指针*/
/*将元素newElem 插入表中的第k 个元素之前，若成功则返回0,否则返回-1*1 /*该插入操作等同于将元素newElem 插入在第k-1 个元素之后*/
{   LinkList p,s;                  /*p、s为临时指针*/
	if(k==1) p=L;                  /*元素newElem 要插入到第1个元素之前*/
	else   p=Find_List(L,k-1);     /*查找表中的第k-1 个元素并令p 指向该元素结点*/
	if(!p) return -1;              /*表中不存在第k-1 个元素，不满足运算要求*/

	s=(NODE*)malloc(sizeof(NODE)); /*创建新元素的结点空间*/
	if(!s) return-1;

	s->data=newElem;
	s->next=p->next;p->next=s;                  /*将元素 newElem 插入第k-1  个元素之后*/
	return 0; 
}/*Insert_List*/

[!example] #【函数】单链表的删除运算#

int Delete_List (LinkList L,int k)      /*L为带头结点单链表的头指针*/
/*删除表中的第k 个元素结点，若成功则返回0,否则返回-1*/
/*删除第k 个元素相当于令第k-1 个元素结点的指针域指向第k+1 个元素所在结点*/
{   LinkList p,q;                   /*p、q为临时指针*/
	if(k==1)p=L;                    /*删除的是第一个元素结点*/
	else p=Find_List(L,k-1);        /*查找表中的第k-1 个元素并令p 指向该元素结点*/
	if(!p||!p->next) return -1;     /*表中不存在第k 个元素*/

	q=p->next;                      /*令q 指向第k 个元素结点*/ /*删除结点*/
	p->next=q->next;    
	free(q);                        /*删除结点*/

	return 0;
}/*Delete_List*/

当线性表采用链表作为存储结构时，不能对数据元素进行随机访问，但是具有插入和删除 操作不需要移动元素的优点。

根据结点中指针域的设置方式，还有其他几种链表结构。

  • #双向链表# 每个结点包含两个指针，分别指出当前元素的直接前驱和直接后继。其特 点是可以从表中任意的结点出发，从两个方向上遍历链表。
  • #循环链表# 在单向链表(或双向链表)的基础上令表尾结点的指针指向链表的第一个结点，构成循环链表。其特点是可以从表中任意结点开始遍历整个链表。
  • #静态链表# 借助数组来描述线性表的链式存储结构，用数组元素的下标表示元素所在结点的指针。

若双向链表中结点的front 和 next 指针域分别指示当前结点的直接前驱和直接后继，则在 双向链表中插入结点*s 时指针的变化情况如图3-4 (a)   所示，其操作过程可表示为：

s->front=p->front;
p->front->next=s;   //或者表示为s->front->next=s;
s->next=p;
p->front=s;

image.png

图3-4 在双向链表插入和删除结点时的指针变化示意图

在双向链表中删除结点时指针的变化情况如图3-4 (b)  所示，其操作过程可表示为：

p->front->next=p->next;
p->next->front=p->front;
free(p);

二、栈和队列

栈和队列是程序中常用的两种数据结构，它们的逻辑结构和线性表相同。其特点在于运算有所限制：栈按“后进先出”的规则进行操作，队列按“先进先出”的规则进行操作，故称为 运算受限的线性表。

1. 栈

栈的定义

栈是只能通过访问它的一端来实现数据存储和检索的一种线性数据结构。换句话说，栈的 修改是按先进后出的原则进行的。因此，栈又称为后进先出(Last In First Out,LIFO)的线性表。在栈中进行插入和删除操作的一端称为栈顶 (Top),   相应地，另一端称为栈底 (Bottom)。 不含数据元素的栈称为空栈。

栈的基本运算。

  1. 初始化栈InitStack(S): 创建一个空栈S。
  2. 判栈空isEmpty(S):当 栈S为空时返回“真”,否则返回“假”。
  3. 入栈Push(S,x): 将元素x 加入栈顶，并更新栈顶指针。
  4. 出栈 Pop(S): 将栈顶元素从栈中删除，并更新栈顶指针。若需要得到栈顶元素的值， 可将Pop(S)定义为一个返回栈顶元素值的函数。
  5. 读栈顶元素Top(S): 返回栈顶元素的值，但不修改栈顶指针。

在应用中常使用上述5种基本运算实现基于栈结构的问题求解。

栈的存储结构

  1. 顺序存储。栈的顺序存储是指用一组地址连续的存储单元依次存储自栈顶到栈底的数 据元素，同时附设指针 top 指示栈顶元素的位置。采用顺序存储结构的栈也称为顺序栈。在这种存储方式下，需要预先定义(或申请)栈的存储空间，也就是说，栈空间的容量是有限的。

因此，在顺序栈中，当一个元素入栈时，需要判断是否栈满(栈空间中没有空闲单元),若栈满，则元素不能入栈。

  1. 栈的链式存储。用链表作为存储结构的栈也称为链栈。由于栈中元素的插入和删除仅在栈顶一端进行，因此不必另外设置头指针，链表的头指针就是栈顶指针。链栈的表示如图3-5所示。
  2. 栈的应用。栈的典型应用包括表达式求值、括号匹配等， 在计算机语言的实现以及将递归过程转变为非递归过程的处理中， 栈有重要的作用。

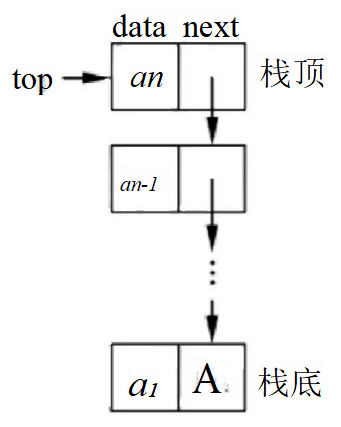
image.png

图3-5 链栈示意图

2.  队列

队列的定义

队列是一种先进先出 (First In First Out,FIFO)的线性表，它只允许在表的一端插入元素，而在表的另一端删除元素。在队列中，允许插入元素的一端称为队尾(Rear),   允许删除元素的一端称为队头 (Front)。

队列的基本运算。

  1. 初始化队列InitQueue(Q):  创建一个空的队列Q。
  2. 判队空 isEmpty(Q):  当队列为空时返回“真”,否则返回“假”。
  3. 入队EnQueue(Q,x):   将元素x 加入到队列Q 的队尾，并更新队尾指针。
  4. 出队DelQueue(Q):   将队头元素从队列Q 中删除，并更新队头指针。
  5. 读队头元素FrontQue(Q): 返回队头元素的值，但不更新队头指针。

队列的存储结构

  1. 队列的顺序存储。队列的顺序存储结构又称为顺序队列，它也是利用一组地址连续的 存储单元存放队列中的元素。由于队列中元素的插入和删除限定在表的两端进行，因此设置队头指针和队尾指针，分别指出当前的队头和队尾。

下面设顺序队列Q 的容量为6,其队头指针为front,  队尾指针为rear, 头、尾指针和队列中元素之间的关系如图3-6所示。
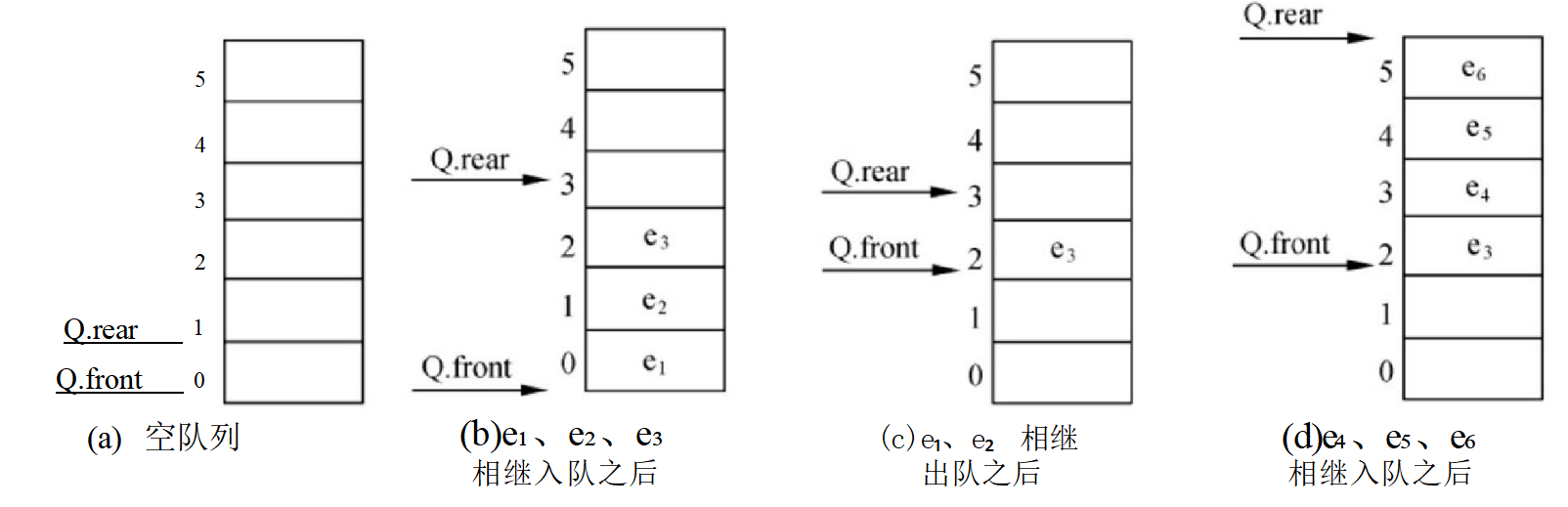
image.png

图3-6 队列的头、尾指针与队列中元素之间的关系

 在顺序队列中，为了降低运算的复杂度，元素入队时只修改队尾指针，元素出队时只修改队头指针。由于顺序队列的存储空间容量是提前设定的，所以队尾指针会有一个上限值，当队尾指针达到该上限时，就不能只通过修改队尾指针来实现新元素的入队操作了。若将顺序队列 假想成一个环状结构(通过整除取余运算实现),则可维持入队、出队操作运算的简单性，如 图3-7所示，称之为循环队列。
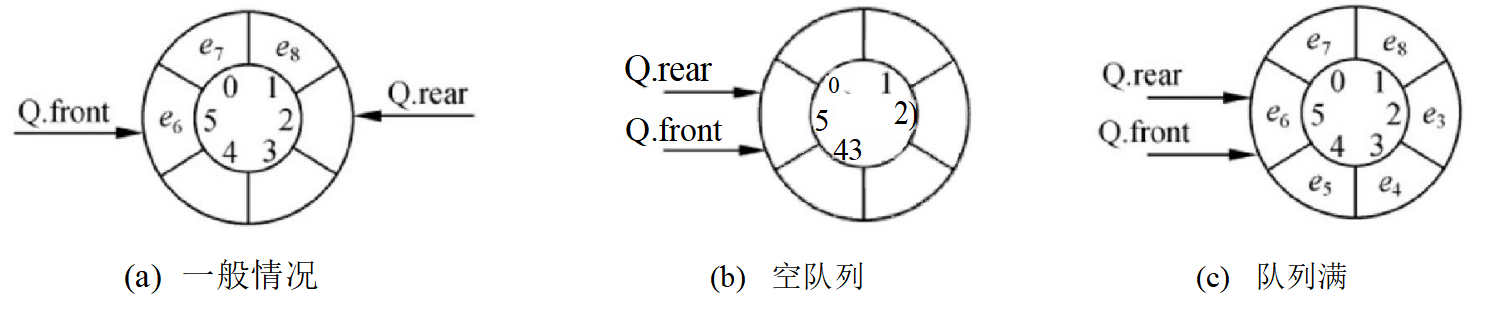
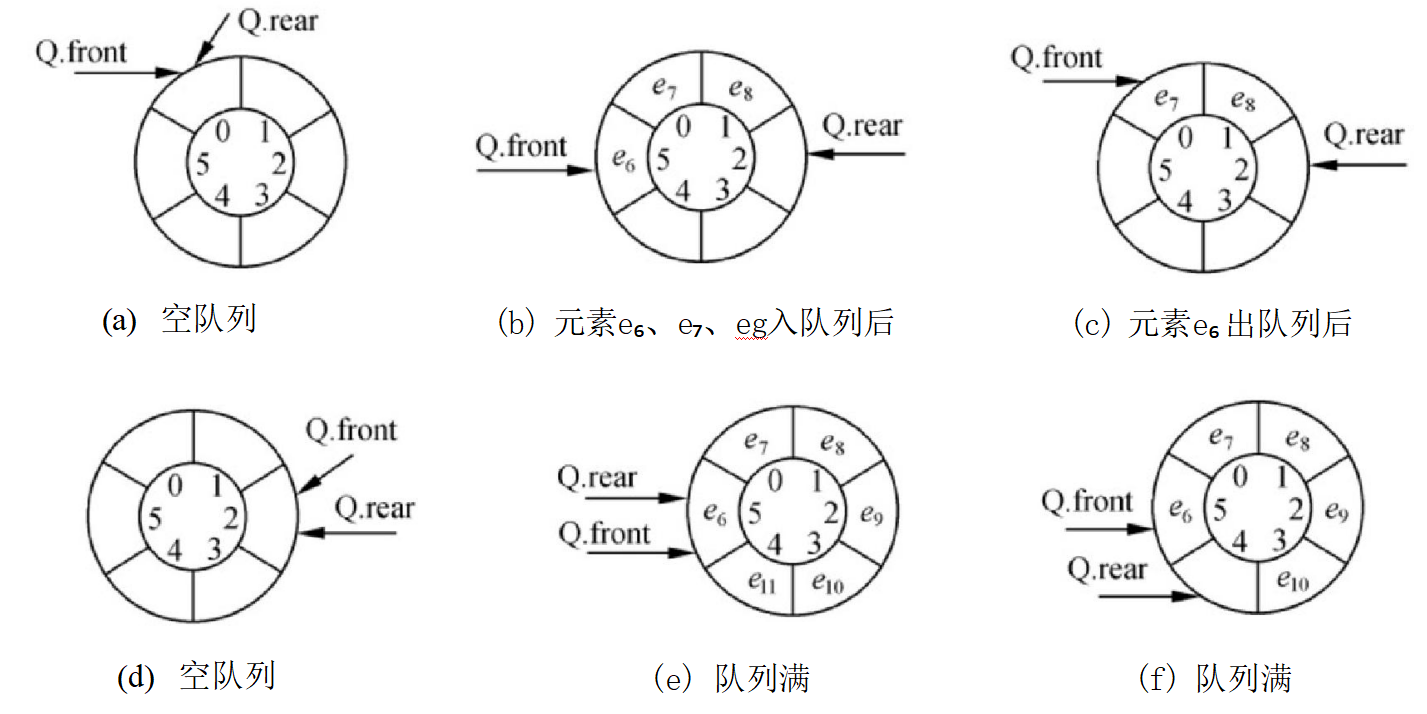
image.png

图3-7 循环队列的头、尾指针示意图

设循环队列Q 的容量为MAXSIZE,  初始时队列为空，且Q.rear 和 Q.front 都等于0,如图 3-8(a)     所示。

元素入队时，修改队尾指针Q.rear=(Q.rear+1)%MAXSIZE,  如图3-8(b) 所示。

元素出队时，修改队头指针 Q.front=(Q.front+1)%MAXSIZE,      如图3 – 8 (c) 所 示 。

根据队列操作的定义，当出队操作导致队列变为空时，则有Q.rear==Q.front,  如图3-8(d) 所示；若入队操作导致队列满，则Q.rear==Q.front,如图3-8(e) 所示。

在队列空和队列满的情况下，循环队列的队头、队尾指针指向的位置是相同的，此时仅仅根据Q.rear 和 Q.front 之间的关系无法断定队列的状态。为了 #区别队空和队满的情况# ，可采用以 下两种处理方式：其一是设置一个标志，以区别头、尾指针的值相同时队列是空还是满；其二 是牺牲一个存储单元，约定以“队列的尾指针所指位置的下一个位置是队头指针时”表示队列 满，如图3-8 (f) 所示，而头、尾指针的值相同时表示队列为空。

image.png

图3-8 循环队列的头、尾指针示意图

设队列中的元素类型为整型，则循环队列的类型定义如下。

#define MAXQSIZE 100 
typedef struct {
	int *base;         /*循环队列的存储空间，假设队列中存放的是整型数*/
	int front;         /*指示队头，称为队头指针*/
	int rear ;         /*指示队尾，称为队尾指针*/
}SqQueue;

[!example] #【函数】创建一个空的循环队列#

int InitQueue(SqQueue *Q)
/*创建容量为MAXQSIZE的空队列，若成功返回0,否则返回-1*/ 
{   Q->base=(int *)malloc(MAXQSIZE*sizeof(int);
	if(!Q->base) return -1;
	Q->front=0;Q->rear=0;return 0;
}/*InitQueue*/

[!example] #【函数】元素入循环队列#

int EnQueue(SqQueue*Q,int e)         /*元素e入队，若成功返回0,否则返回-1*/ 
{   if((Q->rear+1)%MAXQSIZE == Q->front) return -1;
	Q->base[Q->rear]=e;
	Q->rear=(Q->rear+1)%MAXQSIZE; return 0;
}/*EnQueue*

[!example] #【函数】元素出循环队列#

int DelQueue(SqQueue*Q,int *e)
/*若队列不空，则删除队头元素，由参数e 带回其值并返回0，否则返回-1*/
{   if(Q->rear==Q->front) return -1;
	*e=Q->base[Q->front];
	Q->front=(Q->front+1)%MAXQSIZE; return 0;
}/*DelQueue*/
  1. 队列的链式存储。队列的链式存储也称为链队列。这里为了便于操作，给链队列添加一个头结点，并令头指针指向头结点。因此，队列为空的判定条件是头指针和尾指针的值相同，且 均指向头结点。队列的一种链式存储如图3-9所示。
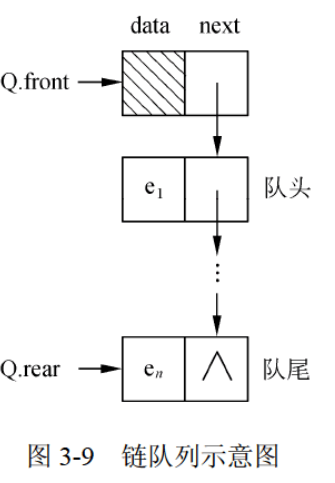
    image.png
    图3-9 链队列示意图
  2. 队列的应用 。队列结构常用于处理需要排队的场合，例如操作系统中处理 打印任务的打印队列、离散事件的计算机模拟等。

三、串

串(字符串)是一种特殊的线性表，其数据元素为字符。计算机中非数值问题处理的对象经常是字符串数据，例如，在汇编和高级语言的编译程序中，源程序和目标程序都是字符串；在事务处理程序中，姓名、地址等一般也是作为字符串处理的。串具有自身的特性，运算时常常把一个串作为一个整体来处理。这里介绍串的定义、基本运算、存储结构及串的模式匹配算法。

1. 串的定义

串是仅由字符构成的有限序列，是一种线性表。 一般记为S='a₁a₂…an',      其 中 ，S 是串名，单引号括起来的字符序列是串值。

2. 串的几个基本概念

  • 空串：长度为零的串称为空串，空串不包含任何字符。
  • 空格串：由一个或多个空格组成的串。虽然空格是一个空白字符，但它也是一个字符，在计算串长度时要将其计算在内。
  • 子串：由串中任意长度的连续字符构成的序列称为子串。含有子串的串称为主串。子串在主串中的位置是指子串首次出现时，该子串的第一个字符在主串中的位置。空串是任意串的子串。
  • 串相等：指两个串长度相等且对应序号的字符也相同。
  • 串比较：两个串比较大小时以字符的ASCII 码值(或其他字符编码集合)作为依据。 实质上，比较操作从两个串的第一个字符开始进行，字符的码值大者所在的串为大； 若其中一个串先结束，则以串长较大者为大。

3. 串的基本操作

  1. 赋值操作 StrAssign(s,t):   将 串s 的值赋给串t。
  2. 连接操作Concat(s,t):   将 串t 接续在串s 的尾部，形成一个新串。
  3. 求串长StrLength(s):   返回串s 的长度。
  4. 串比较StrCompare(s,t):   比较两个串的大小。返回值-1、0和1分别表示 s<t 、s=t  和 s>t 三种情况。
  5. 求子串SubString(s,start,len):   返回串s 中从start 开始的、长度为len 的字符序列。

以上5种最基本的串操作构成了串的最小操作子集，利用它们可以实现串的其他运算。

4. 串的存储结构

串可以进行顺序存储或链式存储。

  1. 串的顺序存储结构。串的顺序存储结构是指用一组地址连续的存储单元来存储串值的字符序列。由于串中的元素为字符，所以可通过程序语言提供的字符数组定义串的存储空间， 也可以根据串长的需要动态申请字符串的空间。
  2. 串的链式存储。当用链表存储串中的字符时，每个结点中可以存储一个字符，也可以存储多个字符，此时要考虑存储密度问题。在链式存储结构中，结点大小的选择会直接影响对串的处理效率。

5. 串的模式匹配

子串的定位操作通常称为串的模式匹配，它是各种串处理系统中最重要的运算之一。子串也称为模式串。

朴素的模式匹配算法

该算法也称为布鲁特—福斯算法，其基本思想是从主串的第一个字符起与模式串的第一个字符比较，若相等，则继续逐一对字符进行后续的比较，否则从主串第二个字符起与模式串的第一个字符重新比较，直到模式串中每个字符依次和主串中一个连续的字符序列相等时为止， 此时称为匹配成功。如果不能在主串中找到与模式串相同的子串，则匹配失败。

[!example] #【函数】以字符串数组存储字符串，实现朴素的模式匹配算法#

int Index(char S[],charT[],int pos)
/*查找并返回模式串T 在主串S 中从 pos开始的位置(下标),若T 不是S的子串，则返回-1*/
/*模式串T 和主串S 第一个字符的下标为0*/ 
{   int i,j,slen,tlen;
	i=pos;j=0;                       /*i、j分别用于指出主串字符和模式串字符的位置*/
	slen=strlen(S);tlen =strlen(T);  /*计算主串和模式串的长度*/
	while (i<slen && j<tlen){
		if(S[i]==T[j]){i++;j++;} 
		else {
			i=i-j+1;                 /*主串字符的位置指针回退*/
			j=0; 
		}
	}/*while*/
	if(j>=tlen) return i-tlen;
	return -1 
}/*Index*/

改进的模式匹配算法

改进的模式匹配算法又称为KMP 算法，其改进之处在于：每当匹配过程中出现相比较的字符不相等时，不需要回退主串的字符位置指针，而是利用已经得到的“部分匹配”结果将模式串向右“滑动”尽可能远的距离，再继续进行比较。

设模式串为"po…Pm-1",KMP匹配算法的思想是：当模式串中的字符p;与主串中相应的字 符S;不相等时，因其前j个字符("po…Pj-1")已经获得了成功的匹配，所以若模式串中的"po…Pk-1" 与"Pj-kPj-1"相同，这时可令pk与S;进行比较，从而使i无须回退。

在KMP 算法中，依据模式串的next函数值实现子串的滑动。若令next[j]=k,则 next[j]表 示当模式串中的pj 与主串中相应字符不相等时，令模式串的Pnext与主串的相应字符进行比较。

next函数的定义如下：
image.png

[!example] #【函数】求模式串的next函数#

void Get_next(char *p,int next[])                     /*求模式串p 的next 函数值并存入数组next*/
{   int i,j,slen;
	slen=strlen(p);i=0; 
	next[0]=-1;j=-1;
	while(i<slen){
		if(j==-1||p[i]==p[j]){++i;++j;next[i]=j;}
		else j=next[i];
	}/*while*/  
}/*Get_next*/

[!example] #【函数】KMP模式匹配算法，设模式第一个字符的下标为0#

int Index_KMP(char *s,char*p,int pos,int next[])
/*利用模式串p 的 next函数，求p在主串s 中从第pos个字符开始的位置*/
/*若匹配成功，返回模式串在主串中的位置(下标),否则返回-1*/ 
{   int i,j,slen,plen;
	i=pos-1; j=-1;
	slen =strlen(s);plen=strlen(p); 
	while(i<slen&&j<plen){
		if  (j==-1||s[i]==p[i]){++i;++j;}
		else j=next[j];
	}/*while*/
	if (j>=plen)return i-plen; 
	else return -1;
}/*Index_KMP*/

例如，设主串为 “abacbcabababbcbc”,  模式串为 “abababb”,  且模式串的next 函数值如下表所示，则KMP 算法的匹配过程如图3-10所示。其中，i 是主串字符的下标，j 是模式串字符的下标。
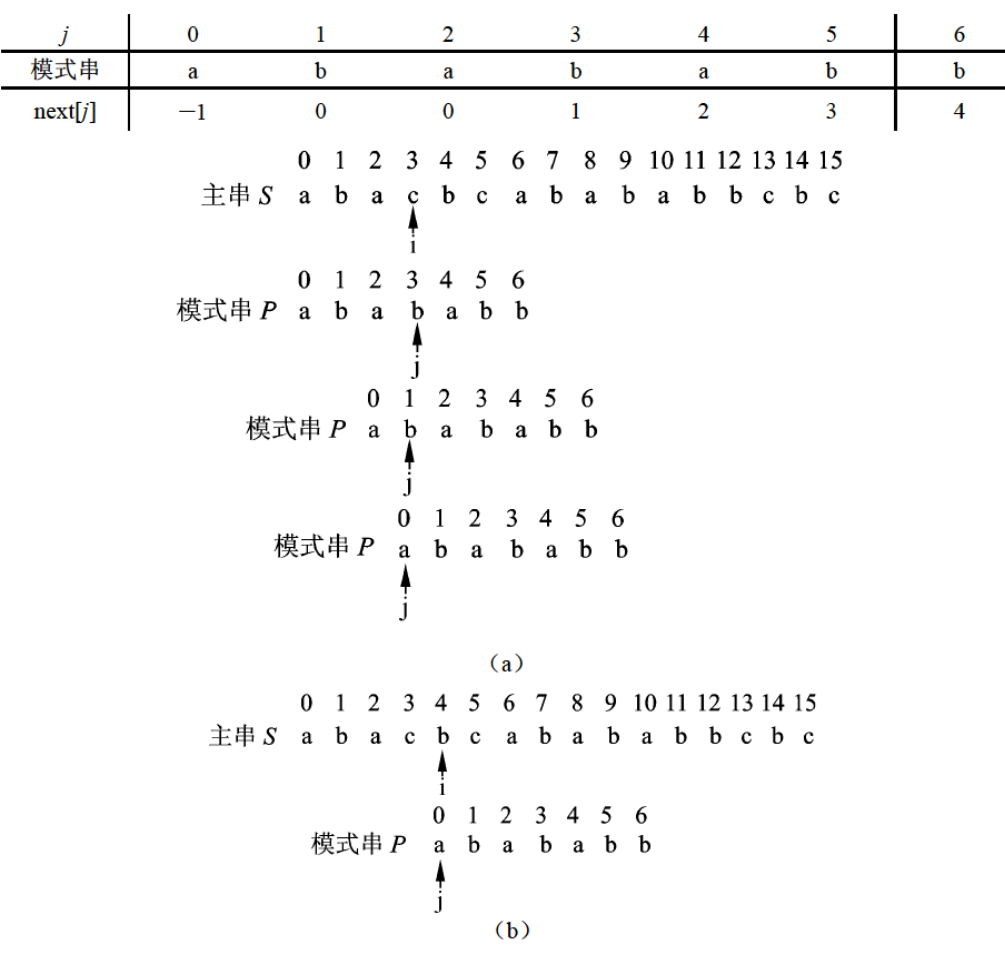
image.png

图3- 10 KMP 模式匹配过程示意图

第一趟匹配从 S[0]与P[0]开始。由于 S[0]=P[0] 、S[1]=P[1] 、S[2]=P[2], 所以接下来比 较 S[3]与P[3],  由于S[3]与P[3]不相等，所以第一趟结束，要进行第二趟匹配，令j=next[3](即 j=1)。第二趟从S[3]与P[1]开始比较，仍不相等，因此第二趟结束，要进行第三趟匹配，所以 令j=next[1]( 即j=0)。第三趟从 S[3]与P[0]开始比较，如图3-10 (a)  所示。由于S[3]与P[0] 不相等，所以令j=next[0]( 即j=-1), 此时满足条件"j==-1",显然不能令 S[3]与P[-1]进行 比较，说明主串中从 i=3 开始的子串不可能与模式串相同，因此需要将i 的值递增后再继续进 行匹配过程，即令i++、j++, 然后下一趟从S[4]与P[0]开始比较，如图3-10 (b)  所示，继续 匹配过程。直到某一趟匹配成功，或者由于在主串中找不到模式串而以失败结束。

© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
分享
喜欢就支持一下吧
点赞7 分享
相关推荐